І. АКТУАЛЬНІСТЬ, МЕТА АВТОРСЬКОЇ ПРАКТИЧНОЇ РОЗРОБКИ

Ця авторська розробка створена з метою отримання практичних навичок вивчення та засвоєння навчального матеріалу шляхом використання актуальних інформаційних технологій на прикладі уроку алгебри, тема якого: «Зв'язок між коренями і коефіцієнтами зведеного квадратного рівняння». 

ІІ. ХІД УРОКУ

1. Сьогодні на уроці:

а) Повторимо пройдений теоретичний матеріал
б) Згадаємо, як розв'язувати квадратне рівняння за допомогою дискримінанта
в) Вивчимо теорему Вієта
г) Застосуємо теорему Вієта для розв'язування вправ

2. Згадай, ти це знаєш!

а) Яке рівняння називають квадратним?
б) Як ми розв'язуємо такі рівняння?
в) Чи всі квадратні рівняння розв'язуються через дискримінант?
г) Які квадратні рівняння називаються неповними?
д) Як ми розв'язуємо неповні квадратні рівняння?
е) Які ще ми знаємо квадратні рівняння?
є) Як вони записуються в загальному вигляді?
ж) Чи можна їх розв'язувати через дискримінант?

Розв'яжіть рівняння

Як називаються квадратні рівняння, після алгебраїчних перетворень?

(зведені, х ²  + рх + q = 0)

Заповніть пропуски в таблиці

Подивіться на таблицю, що ви помітили? Чи допомогла вам ця таблиця в розкритті нових зв'язків між коренями і коефіцієнтами квадратних рівнянь?

3. Зрозумій, це просто!

Теорема:

Якщо зведене квадратне рівняння має два корені, то сума коренів дорівнює другому коефіцієнту рівняння, взятому з протилежним знаком, а добуток коренів – вільному члену.

Теорема називається теоремою Вієта, на ім’я знаменитого французького математика Франсуа Вієта (1540 – 1603). Свою знамениту теорему він довів у 1591 році.

Використовуючи теорему Вієта, заповніть пропуски у формулах:

Доведення теореми Вієта на дошці

Якщо x₁ і x₂ — корені квадратного рівняння ax² + bx + c = 0, то

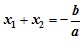
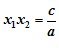
Доведення

Нехай D > 0. Застосовуючи формулу коренів квадратного рівняння, запишемо:

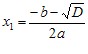
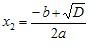
Маємо:

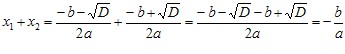
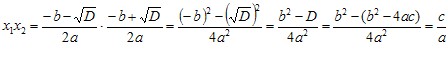
Зауваження:

Теорема Вієта є справедливою й тоді, коли D = 0. При цьому вважають, що

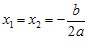
Маємо:

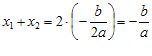
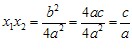
Теорема обернена до теореми Вієта

Якщо числа α і β такі, що

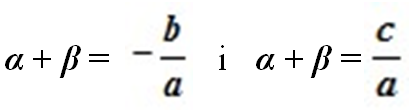
то ці числа є коренями квадратного рівняння ax² + bx + c = 0.

Знайдіть коефіцієнти b і c рівняння х² + bх + с = 0, якщо його коренями є числа -2 і 3

Розв’язання

За теоремою Вієта:

b = - (-2 + 3) = -1
c = -2 ∙ 3 = -6

Відповідь: b = -1 , c = -6

Складіть квадратне рівняння з цілими коефіцієнтами, корені якого   –0,5   і  2   

Розв’язання

Нехай  x₁ = -0,5   і   x₂ = 2 , тоді

x₁ +  x₂  = -0,5 + 2 = 1,5 ,
x₁ ∙ x₂  = -0,5 ∙ 2 =  -1

За теоремою, оберненою до теореми Вієта, числа x₁  і  x₂  є коренями рівняння  х² – 1,5х – 1 = 0

Помноживши обидві частини рівняння на 2, отримуємо квадратне рівняння з цілими коефіцієнтами:  2х² – 3х – 2 = 0

Відповідь: 2х² – 3х – 2 = 0

Число -2 є коренем рівняння  х² – 8х + q = 0 . Знайдіть значення q і другий корінь рівняння.

Розв’язання

Нехай  x₁  і   x₂  корені даного рівняння, причому  x₁  = -2.

За теоремою Вієта:  x₁ +  x₂ = 8 , -2 + x₂  = 8 , x₂  = 10 ;  q = x₁ ∙ x₂  = -2 ∙ 10 = -20

Відповідь:  x₂  = 10 ,  q =  -20

4. Виконай, ти це зможеш!

Складіть квадратне рівняння з цілими коефіцієнтами, корені якого  -1/3  і  2  (Відповідь: 3х² – 5х – 2 = 0)

Один із коренів рівняння х² + 14х + с = 0  дорівнює 7.

Знайдіть другий корінь і число с  (Відповідь: х₂ = -21, с = -147)

Знайдіть корені рівняння x₁ і  x₂  (x₂ >  x₁ ) та вільний член q, якщо х² - 10х + q = 0 і

x₂ -  x₁ = 14  (Відповідь: х₁ = -2, x₂ = 12, q = -24)

ІІІ. ВИСНОВКИ

В результаті застосування викладених у цій авторській роботі матеріалів, учні отримують практичні навички знаходження зв'язку між коренями і коефіцієнтами зведеного квадратного рівняння за допомогою використання актуальних інформаційних технологій. 

 Література

1. Алгебра : підруч. для 8 кл. заліноосвіт. навч. закл. / А.Г. Мерзляк, В.Б. Полонський, М.С. Якір. – Х. : Гімназія, 2016. – 240 с. : іл.;
2. Алгебра : підруч. для 8 кл. загальноосвіт. навч. закл. / Н. С. Прокопенко, Ю. О. Захарійченко, Н. Л. Кінащук. — Х. : Вид-во «Ранок», 2016. – 288 с. : іл.