Якщо учень в школі не навчився сам нічого творити,
то і в житті він завжди буде лише наслідувати, копіювати,
так як мало таких, які б, навчившись копіювати, вміли самостійно застосувати ці відомості
Лев Толстой

Процес набуття знань, умінь, навичок учнями під час дистанційного навчання має індивідуалізований характер. Він відбувається за опосередкованої взаємодії віддалених один від одного його учасників.  Дистанційне навчання на сучасному етапі можна здійснювати за допомогою інформаційно-комунікаційних технологій. Одночасно із швидким розвитком технологій, які дають швидкий доступ до інформації та брак часу до її переосмислення, відбувається деградація інтелектуального розвитку людини. Тому головною метою навчання є не передача знань та інформації, а навчання учнів вмінню мислити. На думку Льва Толстого: «Математика має завданням не навчанню обчисленню, а навчанню людської думки при обчисленні». Саме цю ідею письменника можна ефективно реалізувати, розв’язуючи одну і ту ж задачу різноманітними методами та способами.

У методиці математики методом розв’язування задач називають сукупність прийомів розумової діяльності або логічних математичних дій та операцій, за допомогою яких розв’язується великий клас задач. Поняття «спосіб розв’язування задачі» – вужче. Це сукупність прийомів розумової діяльності або логічних і мате­матичних дій та операцій, які використовують для розв’язування ок­ремої задачі або невеликої сукупності задач певного виду. Оскільки кількість задач, які учні можуть розв’язати в процесі навчання, є обмеженою, учитель має ретельно добирати ці задачі. Слід віддавати перевагу задачам, які будуть найефективнішими для розвитку мислення учня. Розглянемо методи та способи розв’язання однієї задачі, автором якої є відомий письменник Лев Толстой.

Задача. Трава на всьому лузі росте однаково густо і швидко. Відомо, що 70 корів поїли б цю траву за 24 дні, а 30 корів – за 60 днів. Скільки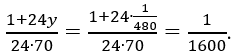 корів поїли б усю траву за 96 днів? (Вважається, що корови поїдають траву рівномірно).

1. Метод розв’язання за частинами (запропонований Я.І.Перельманом [1])

Нехай  –  добовий приріст трави в долях її початкового запасу на лузі. Тоді за 24 доби приріст трави становитиме Якщо загальний запас трави прийняти за одиницю, то за 24 доби корови з’їдять За добу все стадо (70 корів) з’їдає а одна корова з’їдає Аналогічно, з того, що 30 корів поїли б траву того ж лугу за 60 діб, отримаємо що одна корова за добу з’їдає

Тому 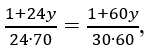звідки Знайшовши величину добового приросту трави, легко визначити, яку долю початкового запасу трави з’їдає одна корова за добу: 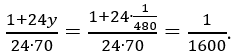 Складаємо рівняння для знаходження невідомого в задачі: якщо шукане число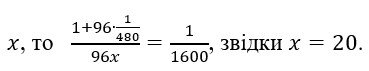Отже, 20 корів поїли б усю траву за 96 днів. Відповідь: 20 корів.

2. Алгебраїчний метод (розв’язання В. Волкова [2])

Часто для розв’язування багатьох задач використовують алгебраїчний метод із застосуванням рівняння або систем рівнянь.

Нехай в початковий момент часу було  m кг трави. Нехай трава росте зі швидкістю  кг/день, а одна корова поїдає траву зі швидкістю  кг/день. 70 корів за 24 дні поїдають  кг трави. З іншого боку вони з’їли всього трави кг. Згідно умови задачі можна скласти наступне рівняння . 30 корів за 60 днів поїдають  кг трави. З іншого боку вони з’їли всього трави  кг. Маємо рівняння Нехай кількість корів, які б поїли всю траву за 96 днів, дорівнює n. Тоді отримаємо рівняння:  
Розв’язавши систему рівнянь

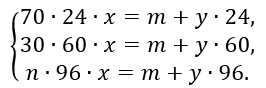
Знаходимо кількість корів Відповідь: 20 корів.

3. Арифметичний метод

Розв’язати складну задачу алгебраїчним методом за допомогою рівняння чи системи рівнянь часто набагато простіше, ніж арифметичним – за допомогою поставлених запитань та арифметичних дій з натуральними числами. Ми переконані, що  відмова в середині ХХ ст. від використання арифметичних методів під час навчання учнів розв’язуванню текстових задач в основній школі, була помилковою. Це призвело до погіршення якості математичної підготовки учнів (в першу чергу 5-6-х класів), зниження їх пізнавальної активності й інтересу до вивчення математики.

Успіх в розв’язанні задачі залежить від уміння ставити до неї запитання. Якщо ви розв’язали задачу, і у вас не виникло запитань, то ви все це зробили даремно. Як же розв’язати задачу без рівняння за допомогою поставлених запитань?

1 спосіб. З умови задачі зрозуміло, що чим більше корів у стаді, тим за меншу кількість діб вони поїдять усю траву, а, отже, вони з’їдять меншу кількість трави. Корови з’їдають траву, що вже росла на лузі і ту, що виросте за певну кількість діб. Покажемо умову задачі на рис. 1: зобразимо у вигляді прямокутників початкову кількість трави на лузі і кількість трави, яка виросла за 24, 60 і 96 діб. З іншого боку один великий прямокутник – це вся маса трави, яку повністю з’їдає стадо за певну кількість днів.  Оскільки за умовою задачі трава росте однаково густо і швидко, то за будь-які 36 днів виросте однакова кількість трави.

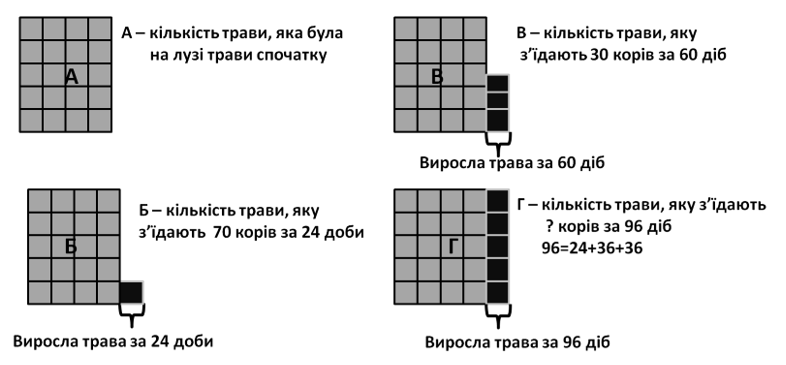
Рис. 1. Кількість трави: А – була на лузі спочатку, Б – з’їдає стадо з 70 корів за 24 доби, В – з’їдає стадо з 30 корів за 60 діб, Г – з’їдає стадо з ? корів за 96 діб

Нехай одна корова з’їдає за добу одиницю маси трави.

1) Скільки трави з’їдять за добу 70 корів?

(одиниць маси)

2) Яку масу трави з’їдять 70 корів за 24 доби?

(одиниць маси)

3) Яку масу трави з’їдять 30 корів за 60 діб?

(одиниць маси)

4) На скільки більше з’їдять трави 30 корів за 60 діб, ніж 70 корів за 24 доби?

(одиниць маси)

Стадо з 30 корів паслося на 36 діб довше, ніж стадо з 70 корів, а, отже, і з’їло трави більше на 120 (одиниць маси). Кількість трави, яка виросла за 36 діб дорівнює 120 (одиниць маси). Стадо корів, яке випасалося 96 діб, їло траву на 36 діб довше, ніж стадо з 30 корів і на 72 доби довше, ніж стадо з 70 корів.

5)  Скільки трави з’їсть стадо, що паслося 96 діб?

(одиниць маси)

6) Скільки корів у стаді, яке з’їдає всю траву за 96 діб?

Відповідь: 20 корів.

2 спосіб. У початковий момент на полі була певна кількість трави А. Якби корови не паслися на лузі, то через 24, 60, 96 діб кількість була б відповідно Б, В, Г (рис.1). Стада з різною кількістю корів поїдають різну кількість трави.

1) За скільки діб 30 корів з’їдять таку ж кількість трави (рис.1, Б), що і 70 корів за 24 доби?

Так як кількість трави Б однакова, то чим більше корів, тим меншу кількість діб вони будуть їсти траву. Тобто, в такому випадку кількість корів та кількість днів є обернено пропорційними величинами.

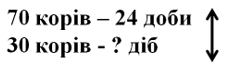
2) На скільки діб стадо з 30 корів з’їсть швидше кількість трави Б, ніж кількість трави В?

 доби

3) За скільки діб 30 корів з’їдять таку ж кількість трави (рис.1, Г), що і стадо з невідомою кількістю корів за 96 діб?

За 4 доби стадо з 30 корів з’їсть стільки трави, скільки її наросте за 36 діб. Так як трава росте постійно однаково, то стадо з 30 корів поїсть усю траву, яка наросте за 96 діб, за

доби

4) Скільки корів у стаді, яке випасалося 96 діб (рис. 4)?

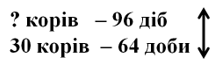
корів

Відповідь: 20 корів.

Висновок. При розв’язуванні задач алгебраїчним способом найважливішим є вміння скласти рівняння або систему рівнянь, які далі розв’язуються за відомими алгоритмами. При використанні арифметичного методу думка працює постійно. Постановка запитань дає змогу проникнути глибше в сутність задачі і розв’язати її кількома арифметичними способами. При цьому з’являються деякі величини, які не задані в умові задачі, але є суттєвими для її розв’язання. До того ж між ними можна виявити цікаві зв’язки, і навіть придумати новий спосіб розв’язання. Так, порівнюючи величини 120 одиниць маси і 4 доби, отримані різними способами, робимо висновок, що 120 одиниць маси з’їсть стадо з 30 корів за 4 доби: Глибину зв’язків між величинами, які знаходять при розв’язанні задачі алгебраїчним методом чи методом за частинами, можна розкрити саме постановкою запитань при розв’язанні задачі арифметичним методом. А це є розвиток мислення, вміння аналізувати, шукати нові зв’язки, відкривати для себе нові способи розв’язання задачі.

Література

1. Перельман Я. И. Занимательная алгебра / Я.И.Перельман. – М.: РИМИС, 2016. – 240 с.
2. 100 тренировочных задач. Задача про коров. Valery Volkov. Назва з екрана [Електронний ресурс]. – Режим доступу: https://www.youtube.com/watch?v=v4qj1EtYa-g
3. Про затвердження Положення про дистанційне навчання : Наказ від 25.04.2013 р. № 466 [Електронний ресурс] / Міністерство освіти і науки України. Режим доступу: http://zakon4.rada.gov.ua/ laws/show/z0703-13.