Тема: Розв’язування  логарифмічних рівнянь.

Мета:

• Навчальна: засвоїти означення логарифмічного рівняння; навчити розв’язувати логарифмічні рівняння різними методами
• Розвиваюча: розвивати вміння розв’язувати логарифмічні рівняння різними способами;
• Виховна: виховувати впевненість у власних силах, необхідність розкривати науковий потенціал;

Компетенції (інформаційно-цифрова компетентність):

• Уміння: структурувати дані; діяти за алгоритмом та складати алгоритми; визначати достатність даних для розв’язання задачі; використовувати різні знакові системи; знаходити інформацію та оцінювати її достовірність; доводити істинність тверджень;
• Ставлення: критичне осмислення інформації та джерел її отримання; усвідомлення важливості ІКТ для ефективного розв’язування математичних задач;
• Навчальні ресурси: візуалізація даних; побудова графіків за допомогою програмних засобів;

Тип уроку: засвоєння нових знань;

Обладнання: опорний конспект, навчальна презентація, мультимедійне обладнання.

Хід уроку

1. Актуалізація опорних знань.

А. Пропонується учням відповісти на поставлені запитання.

• Що називається логарифмом числа за даною основою?
  Очікувана відповідь: Логарифмом числа  за основою  (  і ) називається показник степеня , до якого треба піднести , щоб дістати число .

• Записати основну логарифмічну тотожність?
  Очікувана відповідь: Перерахуйте основні властивості логарифмів ?

Очікувана відповідь:

Т1: Логарифм   добутку двох додатних множників дорівнює сумі їх логарифмів.
Т2: Логарифм частки двох додатних чисел (дробу) дорівнює різниці логарифмів діленого і дільника (чисельника і знаменника).
Т3: Логарифм степеня додатного числа дорівнює показнику степеня , помноженого на логарифм основи цього степеня.
Т4: Логарифм кореня з додатного числа дорівнює логарифму підкореневого виразу, поділеному на показник кореня.

4) Що таке потенціювання?

Очікувана відповідь: Перетворення, за допомогою якого за даним логарифмом числа (виразу) визначають саме число (вираз), називається потенціюванням. Це перетворення є оберненим до логарифмування.

5) Записати формулу переходу від однієї основи логарифма до іншої?
Очікувана відповідь:  

• Які рівняння називають логарифмічними ?
  Очікувана відповідь: Логарифмічними називають рівняння, які містять змінну під знаком логарифма.

• Який вигляд і розв’язок має найпростіше логарифмічне рівняння?
  Очікувана відповідь: Найпростіше логарифмічне рівняння має вигляд  , де , , - будь-яке число. Воно має єдиний розв’язок , який можна дістати за допомогою потенціювання.

• Яка причина появи сторонніх коренів?
  Очікувана відповідь:  Під час розв’язування  логарифмічних рівнянь може статися розширення області визначення і можуть з’явитися сторонні корені.

     Б) Математичний диктант.

Читається кожне завдання окремо. Числові дані записуються на дошці (можна використовувати кодоскоп).

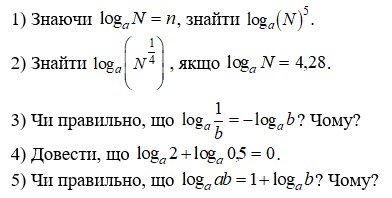
Пропонується учням ( на кожній парті) обмінятися виконаними завданнями і здійснити перевірку диктанту.

Правильні відповіді на всі завдання диктанту демонструються на дошці (були написані попередньо) або за допомогою кодоскопа                                               

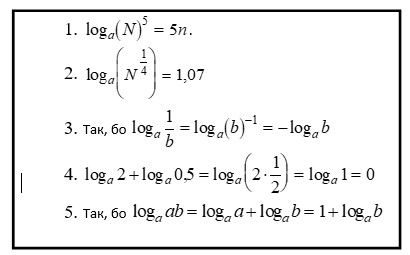
Учні самі виставляють оцінки за такими нормами:  правильно розв’язане завдання - «+», неправильно розв’язане завдання - «-», залежно від кількості «+»  і «-» виставляється оцінка: 5 «+» - «5», 4 «+» - «4»,  3 «+» - «3»,  менше 3 «+»  - 2.

ІІ. Постановка задачі уроку.

Завдання даного уроку - навчитись розв’язувати логарифмічні рівняння різними методами.

ІІІ. Вивчення нового матеріалу .

        А) Первинне застосування набутих знань.

Спочатку нагадуємо, що для розв’язання рівняння (1) досить розв’язати рівняння  (2) і його розв’язки підставити в систему нерівностей 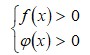 (3), яка задає область визначення рівняння. Коренями рівняння  (1) є тільки ті розв’язки рівняння (2), які задовольняють систему (3), тобто належать області визначення рівняння, заданого формулою (1).

Завдання 1 і 2 розв’язуються колективно під керівництвом вчителя.

Завдання 1: Розв’язання рівняння 

Розв’язання:

Вчитель ставить ряд запитань, щоб проаналізувати розв’язування рівняння.

• Уважно розглянувши праву і ліву частини рівняння, ми бачимо,що основи логарифмів однакові і ми можемо пропотенціювати обидві частини. Що для цього треба зробити?

(Використовуючи властивості Т1: Логарифм   добутку двох додатних множників дорівнює сумі їх логарифмів, Т3: Логарифм степеня додатного числа дорівнює показнику степеня , помноженого на логарифм основи цього степеня, отримаємо

Після потенціювання одержимо Звідси 

• Зробимо перевірку: Підставимо в дане рівняння замість невідомого числа -9. У лівій частині дістанемо вирази 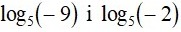, чи може таке бути?

( Вирази не мають смислу, бо логарифми від’ємних чисел не існують)

Отже значення  є стороннім коренем. Тепер перевіримо, чи є коренем даного рівняння число 2. Ліва частина рівняння має вигляд:

Ліва частина дорівнює правій. Отже,  - корінь даного рівняння.

Прийом потенціювання широко застосовується під час розв’язування логарифмічних рівнянь.

Завдання 2: Розв’язати рівняння 

Розв’язання: Скористаємося вже відомим вам методом заміни змінної.

Що нам зручно прийняти за 

Тоді ми дістанемо квадратне рівняння Знаходимо його корені:  Дістанемо два рівняння:

За означенням логарифма знаходимо  розв’язки першого і другого рівняння. (самостійно в зошитах),

За допомогою перевірки з’ясовуємо, що обидва знайдених значення  є коренями даного рівняння. (Перевірку учні роблять самостійно в зошитах).

Відповідь: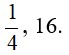

Б) Коментоване розв’язування  вправ.

Завдання 3: Розв’язати рівняння  

Завдання 4: Розв’язати рівняння  

Завдання 5: Розв’язати рівняння  

Завдання 6: Розв’язати рівняння  

Учні розв’язують рівняння самостійно. Більш підготовленому учню вчитель пропонує прокоментувати розв’язування.

Наведемо для прикладу один з можливих варіантів коментування учнем розв’язування рівняння 3. (в залежності від класу вчитель може допомагати при розв’язуванні, підказуючи, якщо виникають складнощі, спосіб розв’язування ).

Це рівняння можна розв’язати за допомогою означення логарифма,  тобто рівняння можна переписати так    і розв’язуємо це рівняння. Отримуємо, що  є коренем рівняння, який належить області визначення рівняння.

  Розв’язання завдання 4: 

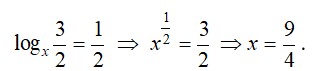
   Відповідь:

Розв’язання завдання 5: Розв’язати рівняння

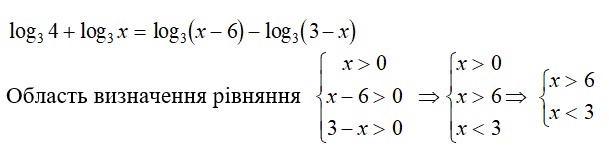
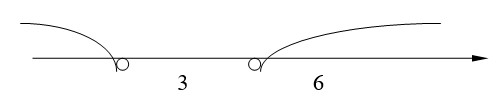
Відповідь: Розв’язків немає.

Розв’язання завдання 6: 

Рівняння такого типу розв’язуються логарифмуванням і називаються показниково-логарифмічними.

Відповідь: 10;  100.

В) Самостійне розв’язування задач .

Завдання 7: Розв’язати рівняння 

Завдання 8: Розв’язати рівняння 

Завдання 9: Розв’язати рівняння

Самостійна робота перевіряється на уроці

ІV. Підсумки уроку.

• Як працював клас.
• Оцінка роботи окремих учнів.

1. Домашнє завдання.

Підручник під редакцією М.І.Шкіль, З.І.Слєпкань, О.С.Дубінчук   «Алгебра і початки аналізу у 10-11 кл.» К: Зодіак-ЕКО,1995р

Розділ V,  №№ 52(8,12,14), 53(1, 2, 3, 6, 11, 16)