Як підвищити кваліфікацію
у центрі прогресивної освіти "Генезум"?

header
  • збірник матеріалів
  • публікація на сайті genezum.org безкоштовна
  • заочна участь
  • для закладів загальної середньої освіти
  • для закладів дошкільної освіти
  • Сертифікат - 5 год, 0.05/0.1 ЄКТС
ПЕРЕЙТИ
header
  • постійний доступ
  • можна проходити у будь-який час
  • дистанційне навчання
  • для закладів загальної середньої освіти
  • для закладів дошкільної освіти
  • Сертифікат - 16/30 год, 0.5/1 ЄКТС
ПЕРЕЙТИ
header
  • безкоштовний перегляд
  • інтерактив зі спікером
  • онлайн формат
  • для закладів загальної середньої освіти
  • для закладів дошкільної освіти
  • Сертифікат - 2 год, 0.06 ЄКТС
СКОРО

Варіант 1
І рівень (3 бали)

 Завдання 1-3 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на вашу думку, відповідь та позначте її.

  1. Оцініть площу квадрата зі стороною а см, якщо 3,1 < а < 3,2.

А)6,2 < S <6,4

Б) 11,4<S<12,8  

В) 9,61<S<10,24     

Г) 12,4 < S < 12,8

 

 
  1. Укажіть нулі функції: у = х² −4х + 3

А) 1

Б) 3

В) −1; −3

Г)   1; 3      

 

 
  1. Знайдіть десятий член арифметичної прогресії ( ), якщо d = - 2.

А)  − 8

Б) - 16

В) 8

Г) − 20

 

 

 ІІ рівень (3 бали)

Завдання 4 передбачає встановлення відповідності. До кожного рядка, позначеного цифрою, доберіть один відповідник, позначений буквою, і поставте позначки в бланку на перетині відповідних рядків (цифри) і колонок (букви).

  1. Установіть відповідність між векторами (1−3) і паралельними їм векторами

     (А−Г), якщо К(2;4), L(1;0), М(0; −1).    


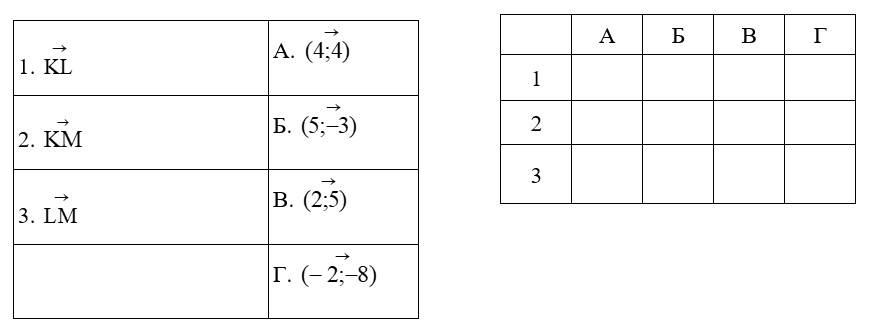
  ІІІ рівень (3 бали)

       Розв’яжіть завдання 5 і 6 та запишіть відповідь.

  1. Розв’яжіть систему нерівностей:

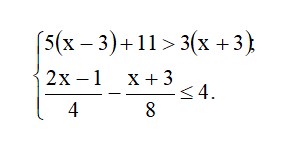
Відповідь:  _______________________________________________________

  1. Бісектриси тупих кутів при основі рівнобічної трапеції ділять її більшу основу на три рівні частини і перетинаються за її межами. Знайдіть відношення середньої лінії цієї трапеції до її більшої основи, якщо градусні міри кутів при основі дорівнюють 120°.

    Відповідь:  _______________________________________________________

ІV рівень (3 бали)

 Обґрунтуйте розв’язання: запишіть послідовні логічні дії та пояснення, зробіть посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.

  1. Розв’яжіть нерівність. 

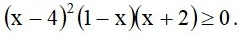
Розв’язання:

Відповідь:  _____________________________________________________

Варіант 2
І рівень (3 бали)

Завдання 1-3 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на вашу думку, відповідь та позначте її.

  1. Оцініть площу квадрата зі стороною а см, якщо 4,2 < а < 4,3.

А) 8,4<S<8,6    

Б) 16,8<S<17,2    

В) 17,64<S<18,49  

Г) 21,6<S<12,9   

 

 
  1. Укажіть нулі функції: у = 8х - х² - 12

А) − 6; − 2

 Б) 2; 6

В) 2

Г) 6

 

 
  1. Знайдіть дванадцятий член арифметичної прогресії ( ), якщо d = 8.

А)  60

Б) 70

В)  90

Г)  80

 

 

 ІІ рівень (3 бали)

Завдання 4 передбачає встановлення відповідності. До кожного рядка, позначеного цифрою, доберіть один відповідник, позначений буквою, і поставте позначки в бланку на перетині відповідних рядків (цифри) і колонок (букви).

  1. Установіть відповідність між векторами (1−3) і перпендикулярними до них векторами (А−Г), якщо А(2;1), В(−1;1), С(3; −2);D(−2; −3).

  ІІІ рівень (3 бали)

 Розв’яжіть завдання 5 і 6 та запишіть відповідь.

  1. Розв’яжіть систему нерівностей: 

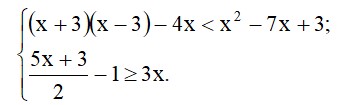
Відповідь:  _______________________________________________________

  1. У прямокутній трапеції більша сторона дорівнює 13 см, середня лінія – 11 см, а площа – 55 см2. Знайти невідомі сторони трапеції.

Відповідь:  _______________________________________________________

ІV рівень (3 бали)

Обґрунтуйте розв’язання: запишіть послідовні логічні дії та пояснення, зробіть посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.

  1. Розв’яжіть нерівність: 

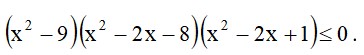
Розв’язання:

Відповідь:  _______________________________________________________

Варіант 3
І рівень (3 бали)

Завдання 1-3 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на вашу думку, відповідь та позначте її.

  1. Оцініть площу квадрата зі стороною а см, якщо 5,4 < а < 5,5.

А) 21 < S < 22            

Б) 29,16 < S < 30      

В) 29,7 < S < 31           

Г) 29,16 < S< 30,25            

 

 
  1. Знайдіть нулі функції: y = x² − 4х + 4

А)  −2; 2

Б) 4

В)  2

Г) − 2

 

 
  1. Знайдіть шістнадцятий член арифметичної прогресії ( ), якщо d = 

А)  139

Б) −131

В)  −139

Г)  131

 

 

 ІІ рівень (3 бали)

Завдання 4 передбачає встановлення відповідності. До кожного рядка, позначеного цифрою, доберіть один відповідник, позначений буквою, і поставте позначки в бланку на перетині відповідних рядків (цифри) і колонок (букви).

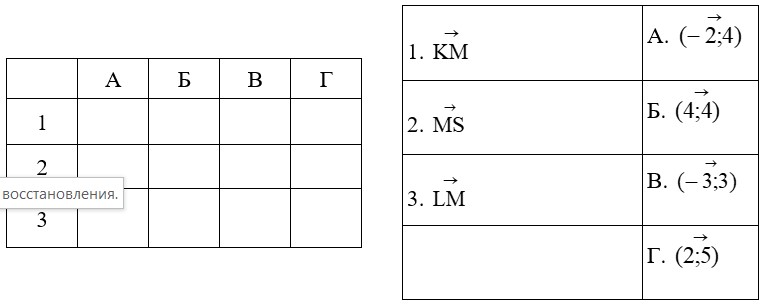
  1. Установіть відповідність між векторами (1−3) і паралельними їм векторами (А−Г), якщо К(2;4), L(1;0), M(0; −1);S(1; −3).

 

ІІІ рівень (3 бали)

Розв’яжіть завдання 5 і 6 та запишіть відповідь.

  1. Розв’яжіть систему нерівностей: 

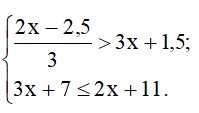
Відповідь:  _______________________________________________________

  1. Продовження бічних сторін AB і CD трапеції ABCD перетинаються в точці К, причому АВ : ВК = 2 : 5. AD – більша основа трапеції. Знайдіть довжини основ трапеції, якщо їх різниця дорівнює 10.

Відповідь:  _______________________________________________________

ІV рівень (3 бали)

Обґрунтуйте розв’язання: запишіть послідовні логічні дії та пояснення, зробіть посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.

  1. Розв’яжіть нерівність: 

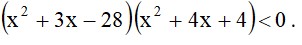
Розв’язання:

Відповідь:  _______________________________________________________

Варіант 4
І рівень (3 бали)

Завдання 1-3 мають по чотири варіанти відповідей, з яких тільки одна відповідь правильна. Оберіть правильну, на вашу думку, відповідь та позначте її.

  1. Оцініть площу квадрата зі стороною а см, якщо 4,2 < а < 4,3.

А) 17,76<S<18,49      

Б) 11,4<S<12,8     

В) 18,06<S<19,8       

Г) 11,4<S<12,8       

 

 
  1. Знайдіть нулі функції: у = х² −7х−18

А) − 2

Б) 9

В) −2; 9

Г) – 9; 2

 

 
  1. Знайдіть чотирнадцятий член арифметичної прогресії ( ), якщо

     d = - 7.

А)  − 88

Б) − 94

В)  88

Г)  94

 

 

 ІІ рівень (3 бали)

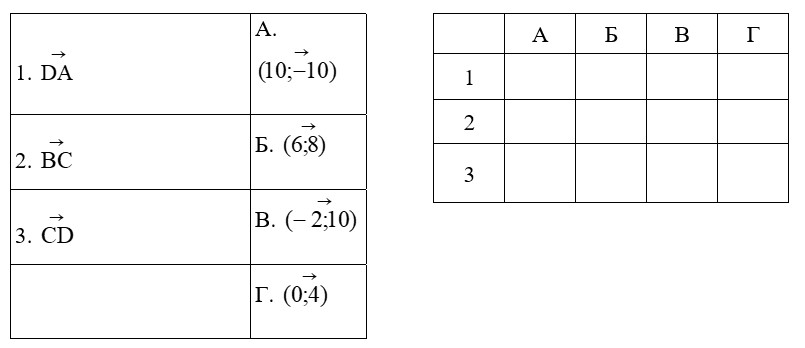
Завдання 4 передбачає встановлення відповідності. До кожного рядка, позначеного цифрою, доберіть один відповідник, позначений буквою, і поставте позначки в бланку на перетині відповідних рядків (цифри) і колонок (букви).

  1. Установіть відповідність між векторами (1−3) і перпендикулярними до них векторами (А−Г), якщо А(2;1), В(−1;1), С(3; −2);D(−2; −3).

ІІІ рівень (3 бали)

Розв’яжіть завдання 5 і 6 та запишіть відповідь.

  1. Розв’яжіть систему нерівностей: 

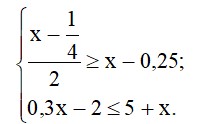
Відповідь:  _______________________________________________________

  1. Продовження бічних сторін AB і CD трапеції ABCD перетинаються в точці L, причому LC : CD = 3 : BC – менша основа трапеції. Знайдіть довжини основ трапеції, якщо її середня лінія дорівнює 21.

Відповідь:  _______________________________________________________

ІV рівень (3 бали)

Обґрунтуйте розв’язання: запишіть послідовні логічні дії та пояснення, зробіть посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.

  1. Розв’яжіть нерівність: 

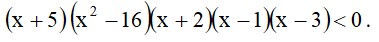
Розв’язання:

Відповідь:  _______________________________________________________