Завдання зовнішнього незалежного оцінювання обов’язково включають рівняння чи нерівність з параметром або їх системи. В шкільному курсі математики для старшої школи (рівень стандарту) зовсім мало уваги приділяється розв’язуванню таких завдань, які для більшості учнів є складними. Проте їх зміст не виходить за межі програми. Завдання з параметрами відкривають широкі можливості для математичного розвитку особистості, логічного мислення, застосування властивостей функцій, геометричних прийомів розв’язання задачі в нестандартних ситуаціях. 

Рівність із змінною називається рівнянням. Розв’язати рівняння – значить знайти всі його корені (розв’язки) або показати, що їх немає. Коренем (або розв’язком) рівняння називається значення змінної, що перетворює рівняння на правильну числову рівність. Лінійним рівнянням з однією змінною називають рівняння виду , де  – змінна,  і  – відомі числа. Якщо в рівнянні, крім букв, що позначають невідомі, є одна або кілька інших букв, то таке рівняння називають з буквеними коефіцієнтами. Буквені коефіцієнти в рівнянні називають параметрами. Розв’язати рівняння з параметром означає знайти його корені для всіх значень параметра. Рівняння з параметрами розв’язують так само, як і рівняння без параметрів, але лише доти, доки кожне перетворення можна виконати однозначно. Якщо ж якесь перетворення не можна виконати однозначно, то розв’язання потрібно розбити на різні випадки залежно від значень параметра. При розв’язуванні таких завдань зручно користуватися загальними алгоритмами та їх блок-схемами. Алгоритм – набір інструкцій, які описують порядок дій виконавця, щоб досягти результату розв’язання за скінченну кількість дій. Властивості алгоритму: дискретність, визначеність, зрозумілість, масовість, формальність, результативність. Для наочного представлення структури алгоритмів використовують блок-схеми.

Будь-яке лінійне рівняння з параметром можна звести до рівняння виду , де  і  – деякі числа. Рівняння виду  має такий алгоритм розв’язання  (рис. 1):

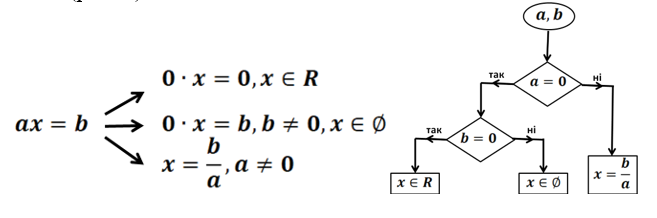Рис. 1. Алгоритм та його блок-схема розв’язання рівняння виду

Приклад 1. Знайти всі корені рівняння  в залежності від параметра .

Розв’язання. Перетворимо праву частину рівняння:

Нехай

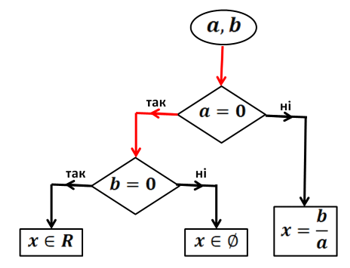
Рис. 2. Випадок, коли в рівнянні  .

Якщо  

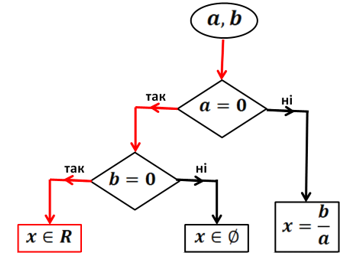
Рис. 3. Випадок, коли в рівнянні .

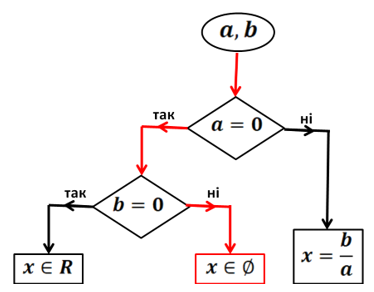Рис. 4. Випадок, коли в рівнянні  .

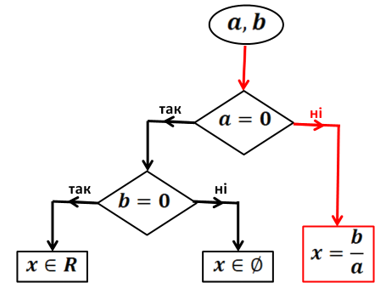
Рис. 5. Випадок, коли в рівнянні .

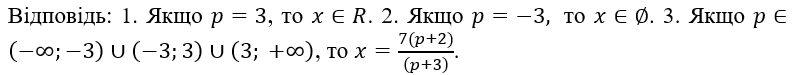
Для розв’язування квадратного рівняння виду зручно використати наступну блок-схему (рис. 6).

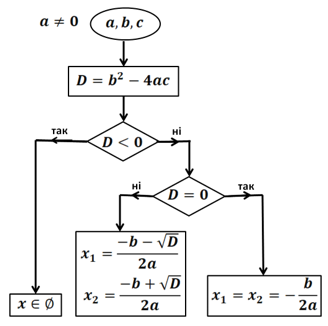
Рис. 6. Блок-схема розв’язування квадратного рівняння

Приклад 2. Знайти всі корені рівняння  в залежності від параметра .

Розв’язання. Позначимо

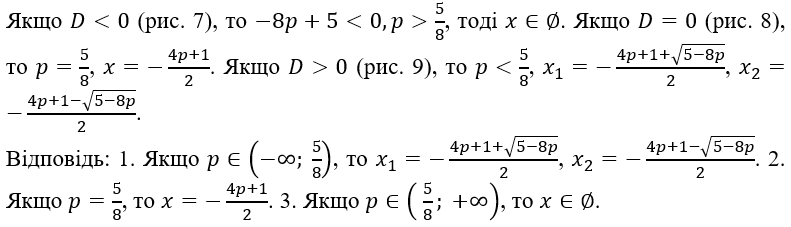
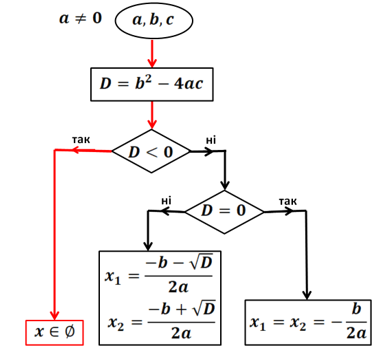
Рис. 7. Випадок, коли в квадратному рівнянні

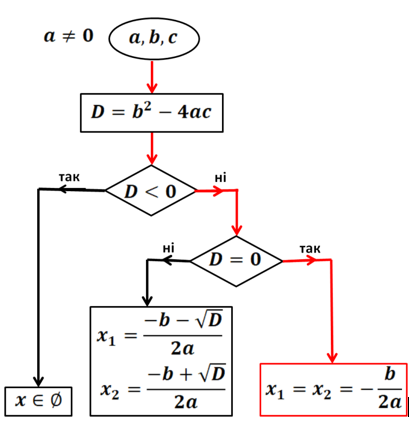
Рис. 8. Випадок, коли в квадратному рівнянні

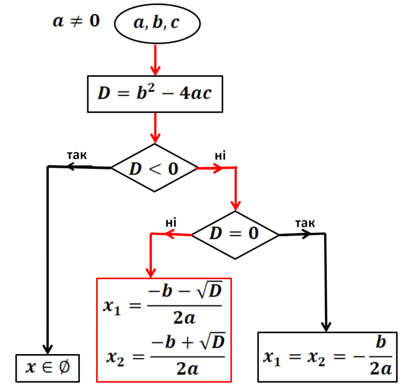
Рис. 9. Випадок, коли в квадратному рівнянні

Розв’язання рівняння виду  з параметром слід розпочинати із запитання: «А чи є рівняння квадратним?» Якщо коефіцієнт    набуває нульового значення, то рівняння  перетворюється в лінійне рівняння (рис. 10).

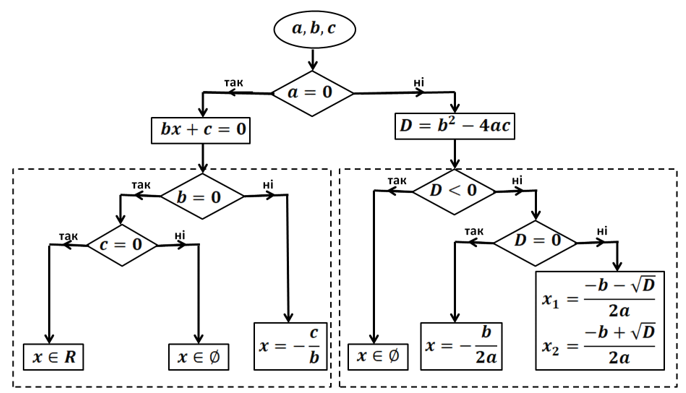
Рис. 10. Блок-схема розв’язування рівняння виду

Приклад 3. Знайти всі корені рівняння  в залежності від параметра .

Розв’язання

Нехай

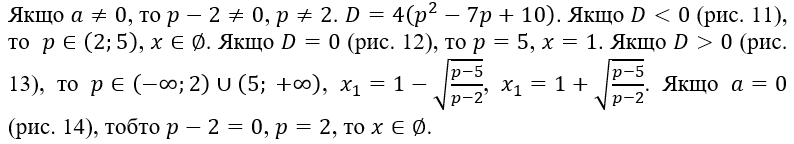
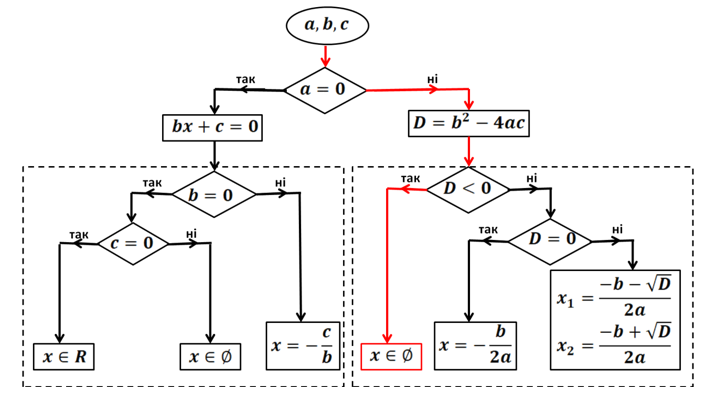
Рис. 11. Блок-схема розв’язування рівняння

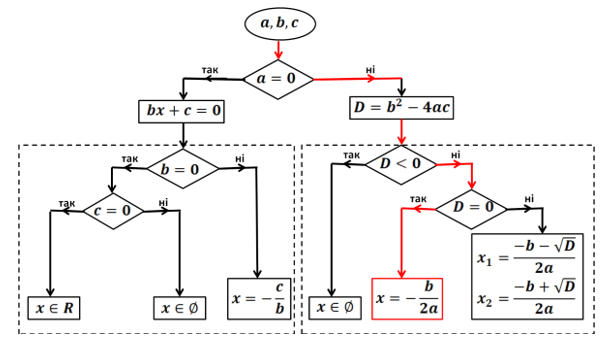
Рис. 12. Блок-схема розв’язування рівняння

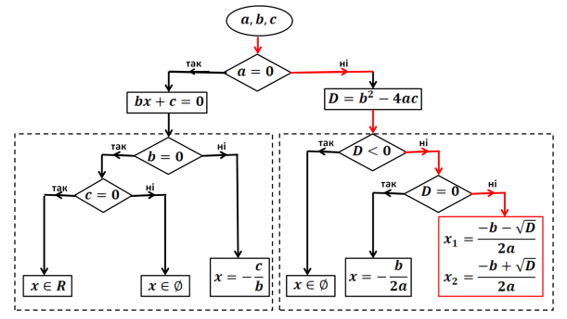
Рис. 13. Блок-схема розв’язування рівняння

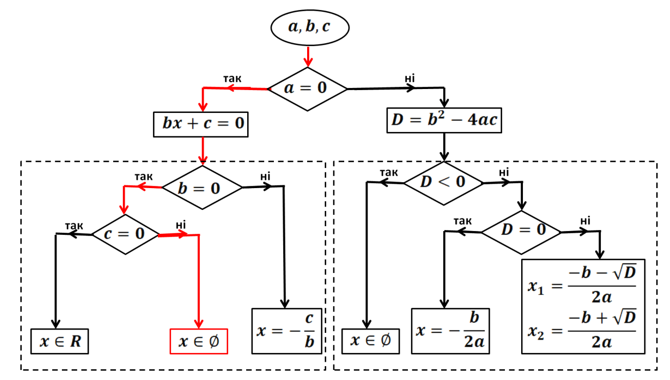
Рис. 14. Блок-схема розв’язування рівняння

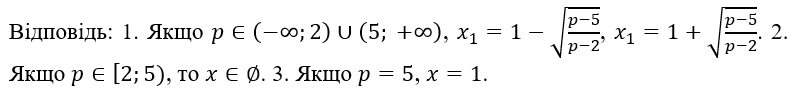
Висновок. Застосування запропонованих алгоритмів та їх блок-схем для розв’язування рівнянь, які зводяться до виду   значно спрощує розв’язання, яке на перший погляд здається складним і незрозумілим. Процес розв’язання перетворюється на послідовне виконання простих кроків, що дає можливість дослідити кількість коренів в залежності від значень параметрів і отримати повний розв’язок рівняння з усіма коренями.

Література

1. Горнштейн П.И. Задачи с параметрами / П.И.Горнштейн, В.Б.Полонский, М.С.Якир. – К.: РИА «Текст»; МП «ОКО», 1992. – 290 с.
2. Математика. Комплексна підготовка до ЗНО і ДПА / Уклад.: А.Капіносов [та ін.]. – Тернопіль: Підручники і посібники, 2019. – 512 с.
3. Мерзляк А.Г. Алгебра: підруч. Для 7 кл. загальноосвіт. навч. закладів – А.Г.Мерзляк, В.Б.Полонський, М.С.Якір. – Х.: Гімназія, 2018. – 256 с.: іл.
4. Нелін Є.П. Алгебра в таблицях: Навч. посібник для учнів 7 – 11 класів / Є.П.Нелін. – Х.: Світ дитинства, 2000. – 116 с.