На підставі сучасних досліджень психологів встановлено, що сучасних дітей і підлітків не влаштовує роль пасивних слухачів на уроці. Вони чекають незвичайних форм знайомства з новим матеріалом, в яких могли б утілитися їх активність, діяльний характер мислення, тяга до самостійності, і саме ігрові технології сприяють реалізації цих потреб учнів.

У сучасній школі виникає насущна потреба в розширенні методичного потенціалу в цілому і в активних формах навчання зокрема.

Ігрові технології є однією з унікальних форм навчання, яка дозволяє зробити цікавим і захоплюючим не лише роботу учнів на творчо-пошуковому рівні, але і буденні кроки по вивченню різноманітних технологій [7. с.180-193].

Організовуючи ігри на уроках доцільно їх поєднувати з іншими видами навчально-пізнавальної діяльності підлітків, добираючи раціональні та ефективні методи і форми проведення дидактичних ігор, визначаючи місце для їх проведення, можна значно підвищити педагогічну ефективність уроків математики в 5-9-х класах за рахунок стимулювання навчально-пізнавальної активності учнів [6, с. 128].

Тож мета роботи це пошук, розробка і перевірка навчально-методичних умов формування й розвитку мислення учнів через ігрові технології  на уроках математики.

Досвід викладання математики показує, що всі ці завдання можна легко розв’язати, якщо учитель зможе перетворити свій урок на свято пізнання, а допоможе йому в цьому дидактична гра.

Правильно підібрані й добре організовані ігри, логічні задачі, вправи для розвитку уяви, пам’яті, уваги сприяють всебічному гармонійному розвитку школярів, допомагають виробити необхідні в житті й навчанні корисні навики і якості.

Гра – це «чарівна паличка», за допомогою якої можна навчити дитину читати, писати, і, головне, мислити, винаходити, доводити. Важливо, щоб гра захоплювала й була доступною, щоб у ній був елемент змагання, якщо не з кимсь, то, принаймні, з самим собою.

Звичайно, коли діти відгадують головоломку, логічні завдання, вони, як правило, застосовують метод проб і помилок, перебираючи різноманітні варіанти.

У північних народів є простий і мудрий афоризм: «Якщо подарувати людині одну рибину, вона буде ситою один день. Якщо подарувати дві, буде ситою два дні. А якщо навчити ловити рибу – буде ситою все життя.» Так і в навчанні: скільки б у школяра не було предметних знань і вмінь, старанності, сумлінності – їх усе одно буде замало для подальшого успішного навчання й розвитку[2, с. 145].

Кожному важливо навчитися аналізувати, відрізняти гіпотезу від факту, чітко виражати свої думки, а з іншого боку - розвити уяву й інтуїцію (просторове бачення, здатність передбачати результат і вгадати шлях рішення). Саме математика надає сприятливі можливості для виховання волі, працьовитості, наполегливості в подоланні труднощів, завзятості в досягненні цілей [4, с. 4].

Для учнів середньої ланки актуальним будуть загадки та кросворди. Наприклад для учнів 5-го класу при вивченні теми «Звичайні дроби» можна запропонувати кросворд розгадавши який у виділених клітинках ви прочитаєте з якою галуззю пов’язані звичайні дроби.

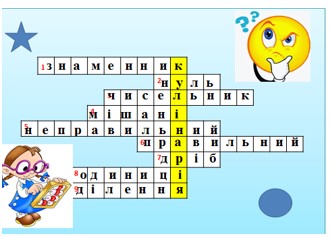Також можна розв’язати цікаві задачі на приготування піци (заготовки можна зробити із кольорового паперу). Наприклад:

А на домашнє завдання можна запропонувати придумати задачу приготування солодкої піци.

У 9-му класі під час актуалізації опорних знань з теми: «Застосування тригонометричних функцій до знаходження площ» можна представити плакат на якому намальована модель сукні (яка складається з різних фігур), а учням потрібно під відповідними фігурами прикріплювати картки з формулами площ даних фігур.

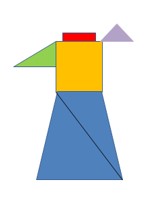Для учнів 6-го класу можна запропонувати завдання:

При вивченні у 7 класі найпростіших фігур пропонується завдання: яка з наведених фігур зайва?

ПРЯМА, ВІДРІЗОК, ТРИКУТНИК, ПРОМІНЬ.

Також можна застосувати гру «Пазли»

Учням пропонується чи то індивідуально, чи в парах скласти цілісну картинку, щоб утворилось математичне твердження.

сума, суміжний, кут, градус, 180, рівність.(Відповідь:Сума суміжних кутів дорівнює 180⁰.)

Висновок. Сьогодні математика як жива наука з різнобічними зв'язками, що істотно впливає на розвиток інших наук і практики, є базою науково-технічного прогресу й важливим компонентом розвитку особистості.

Одніми з основних цілей вивчення математики є формування й розвиток мислення дитини, насамперед, абстрактного мислення, здатності до абстрагування й уміння «працювати» з абстрактними, «невловимими» об'єктами. У процесі вивчення математики в найбільш чистому виді може бути сформоване логічне (дедуктивне) мислення, алгоритмічне мислення, багато якостей мислення ‒ такі, як сила і гнучкість, конструктивність і критичність і тощо [3, с. 54].

Основною метою математичної освіти повинен бути розвиток уміння математично, а значить, логічно й усвідомлено досліджувати явища реального світу. Реалізації цієї мети може й повинне сприяти застосування на уроках математики різного роду ігор та задач

Отже, ігрові моменти на уроках здатні зацікавити учнів до вивчення математики й розширити мислення дитини.

Таким чином, використання вчителем  ігор на уроках математики і в позаурочний час є не тільки бажаним, але навіть необхідним елементом навчання математики.

Література

1. Білокобильська Н. Розвиток логічного мислення // Початкова освіта. – 2000. – C. 137.
2. Веретенко Т. Г. Загальна педагогіка: Навчальний посібник для студентів педагогічних спеціальностей вузів / Т. Г. Веретенко. – К. : Професіонал, 2004. – C.145.
3. Слєпкань З.І. Методика навчання математики: Підручник. 2 - ге вид., доп. І переробл. К.: Вища шк., 2006. – C. 54.
4. Стеценко І. Логіка світу // Початкова освіта. – 2001. – № 35. – С. 4.
5. Соловйова Л.О. Ігрові форми навчання як засіб активізації пізнавальної діяльності учнів.// Математика. – 2007. - №16-18. – С.2-9.
6. Тополя Л., Швець В. Дидактичні ігри на уроках алгебри та геометрії. 7–9 класи. – К.: Шк. Світ, 2009. – C. 128 – (Бібліотека «Шкільний світ»).
7. Шарко В.Д. Сучасний урок. – К.,2006. – С.180-193.