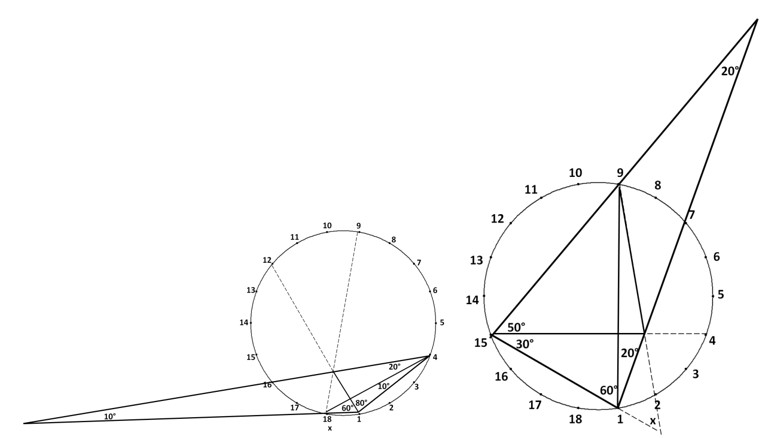
Кожен поважаючий себе любитель геометрії намагався розв’язувати «незручні» задачі на визначення невідомих кутів трикутника. Деякі з найвідоміших наведені на рис. 1. Задачі не прості, звичайним обчисленням не піддаються! Тому і є такими захоплюючими! Такі задачі схожі на те, що з певної конструкції взята якась деталь і пропонується вирішити: що це і звідки? Такі задачі традиційними, стандартними способами розв’язати досить складно. Звичайно, придумані способи розв’язання для окремих задач. Але, якщо незначно змінити умову задачі, то попередні способи не працюють.

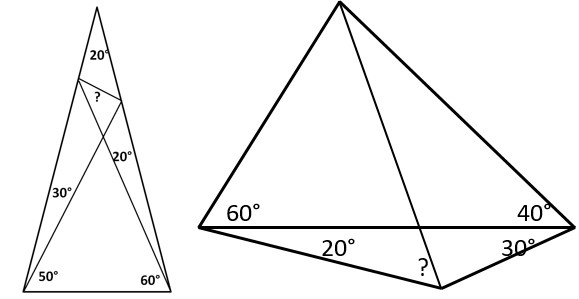
Рис. 1. Задачі на визначення невідомих кутів в трикутника

Як же автори таких задач «підбирали» значення кутів для трикутника? Як таке можна придумати, а тим більше розв’язати? Психологи говорять, щоб розв’язати проблему (задачу) потрібно вийти за межі цієї проблеми (задачі). Усе в цьому світі складається з певних частин і саме є частиною чогось більшого, яке ми часто не можемо відразу уявити чи усвідомити як окремий елемент.

У статті пропонується підхід до розв’язання «незручних» задач у сукупності їх взаємозв’язків з іншими конструкціями. У чому може гармонійно міститися трикутник? Звичайно – це коло! Коло, описане навколо трикутника, яке містить вписані кути, кути між хордами. Але цього замало! Якщо проаналізувати значення кутів трикутника «незручної» задачі, то деякі з них мають дільником числа 10, 20, інші 6, 12, 24, 15, 30, чи 9, 18. Де в колі такі кути? Це – вписані, центральні кути або кути між хордами. Придивившись до чисел 10, 20, 6, 12, 24, 15, 30, 9, 18, 36, робимо відкриття: всі вони є дільниками 360°. Що це може бути? Правильний n-кутник з деякими його діагоналями, що є хордами кола. Найбагатшим на приємні сюрпризи є правильний 18-кутник. Отже, трикутник з невідомими кутами пропонуємо вписати в коло. У чому привабливість запропонованого методу?

• Розв’язання містить мінімальну кількість кроків
• Трикутник розглядається як елемент правильного n-кутника: сторони –діагоналі та відрізки – діагоналі
• Усі прямі і відрізки (та їх продовження) проходять лише через певні точки, що є вершинами n-кутника
• Цілочисельні значення всіх кутів.

Як приклад, розглянемо задачу з невідомим кутом х (рис. 2). Стандартний метод її роз’язання є досить громіздким. А за допомогою 18-кутника розв’язання задачі містить один крок:

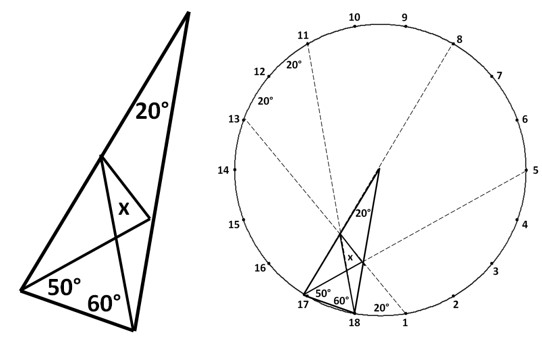Рис. 2. Сторони та деякі елементи трикутника є частинами діагоналей 18-кутника

Важливішим завданням є знайти відповідь на запитання «Як таку задачу «придумати»?» Що ж роблять «видумщики» таких задач? Те, що й фокусники: зосереджують увагу глядача (того, хто буде розв’язувати) на одному, старанно приховуючи важливіше: те, що пояснить фокус (метод, спосіб розв’язання). Якщо глядач зрозуміє суть фокусу, то і сам зможе його показувати, і, навіть, більше – сам зможе придумати нові фокуси. Тобто самому можна придумати задачі, яких ще не було (авторські задачі)!

Найважливішим для розуміння і створення таких задач є відшукання у правильному n-кутнику трьох діагоналей, що перетинаються в одній точці. Такі діагоналі зручно знаходити у правильному 18-кутнику, вписаному в коло. Ділимо коло на 18 рівних частин. Точки поділу будуть вершинами правильного 18-кутника. Знаходимо три діагоналі (хоча б дві відмінних від діаметра), що перетинаються в одній точці. Вибираємо вершини трикутника так, щоб принаймні дві з них були вершинами 18-кутника, а проведені відрізки були частинами діагоналей. Виділяємо трикутник з його елементами і цю конструкцію віддаляємо від правильного многокутника, вписаного в коло. Задача готова! Така схема складання задач проілюстрована на рис. 3 – 5.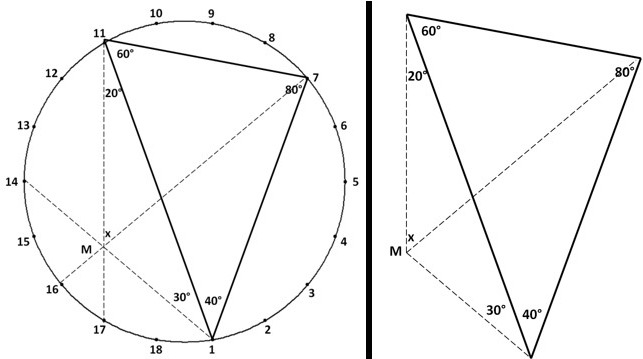

Рис. 3. Задача з точкою М поза трикутником

За трикутником взята точка М така, що проведені відрізки з цієї точки до вершин, утворюють кути 20° і 30°. Розв’язання до задачі:,  – діаметр кола.

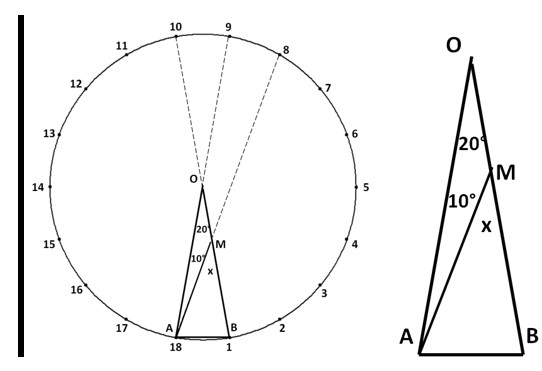 Рис. 5. Одна з вершин трикутника є центром кола

Розв’язання: будуємо хорди 1-10, 9-18, 8-18. 

Конструктор авторських задач

Конструктором для створення задач є многокутник, вписаний в коло, та його діагоналі, що перетинаються в одній точці (рис. 6).

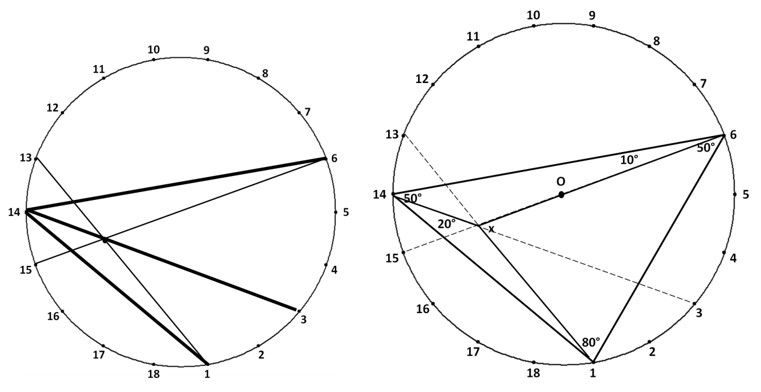Рис. 6. Точка перетину трьох діагоналей 18-кутника та задача, створена за допомогою цього конструктора

Розв’язання: 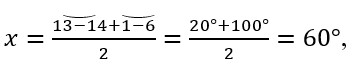6-15 – діаметр кола.

Використавши 24-кутник, можна придумати задачі з кутами кратними п’яти. Приклад такої задачі представлено на рис. 7. Розв’язання:1-12, 9-19, 11-23 – діагоналі, що перетинаються в одній точці.

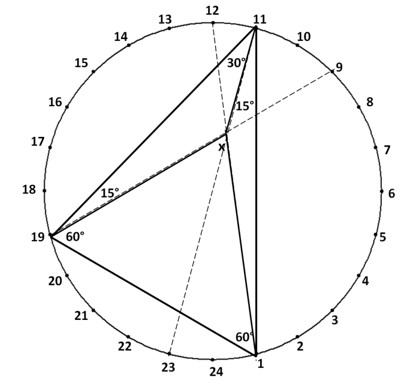Рис. 7. Конструктор з 24-кутником

У наступній задачі необхідно довести, що відрізки АВ і МN паралельні. Це легко зробити за допомогою 18-кутника (рис. 8):

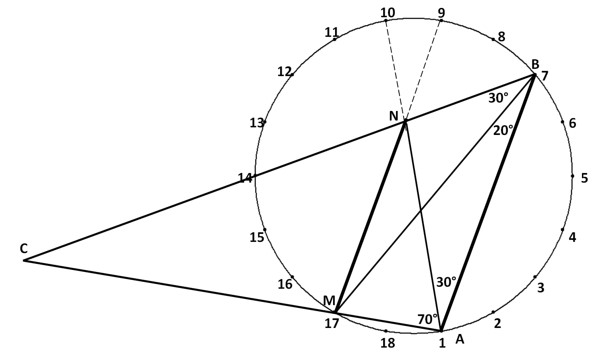
Рис. 8. Конструктор з 18-кутником

Запропонований конструктор задач дає змогу вийти за межі «меж», якщо дві вершини трикутника лежать на колі, а третя поза колом. Розв’язання таких задач (рис. 9): у трикутнику кути 10°, 30°, 140°, діагоналі 1-12, 9-18, 4-16,  (задача 1), діагоналі 1-7, 2-9, 4-15,   (задача 2).

 Задача 1                                                                           Задача 2

Рис. 9. Вийти за межі «меж»: задача 1 і задача 2

У задачі (рис. 10) трикутник з невідомим кутом можна розмістити в коло двома способами. Можна використати конструктор з 30-кутником (рис. 11)

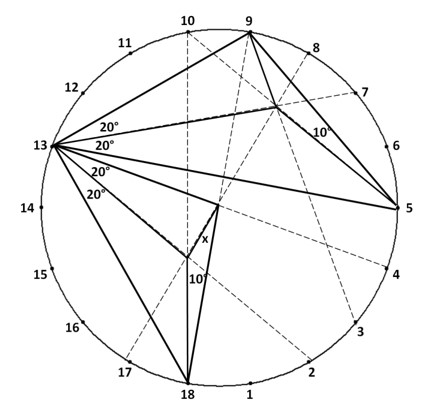 Рис. 10. Два способи розміщення трикутника в колі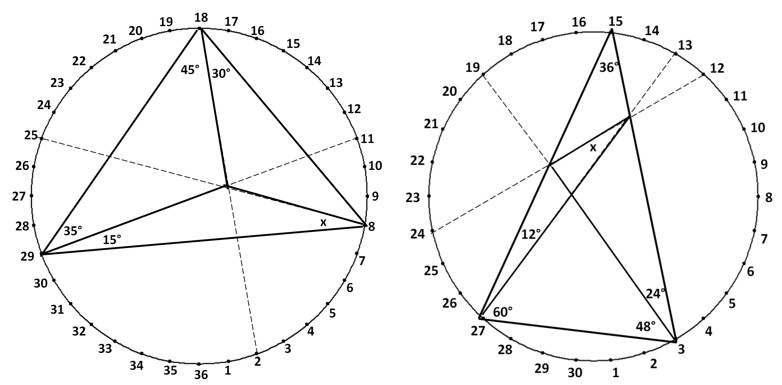

Рис. 11. Конструктор з 36-кутником 30-кутником

Висновок. Сутністю таких задач є дискретність значень кутів, яку визначає кількість сторін правильного n-кутника. За рахунок чого проявляється дискретність? Вершини n-кутника визначають хоча б дві вершини трикутника. Решта відрізків є частинами діагоналей. Якщо одна з вершин не належить колу, то дві сторони трикутника міститимуть вершини n-кутника. Значення величин кутів визначають за центральними вписаними кутами та кутами між хордами.

Література

1. Прасолов В. Диагонали правильного 18-угольника / В.Прасолов // Квант. – 1991. – № 5. – С. 40-42.
2. Прасолов В.В. Задачи по планиметрии / В.В.Прасолов. – М.: Наука, 1991. – 320 с.
3. Математика. Задача про треугольник с углами 20, 80, 80. Бермудский треугольник в геометри. Назва з екрана [Електронний ресурс]. – Режим доступу: https://www.youtube.com/watch?v=P-MifROTIDk